Appendix: Fibonacci numbers … and more
Fibonacci numbers are the members of a series formed in the following way. We start with 1. Then add 1 and get 1 + 1 = 2. Then we add 1 to 2 and get 3. The general formula is: take the (n – 1)th member, add it to the nth member to obtain the (n + 1)st member. Therefore, the Fibonacci numbers are
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …..
But we may start with any other two (positive) numbers. This is what we will obtain if we start with 1 and 3:
1, 3, 4, 7, 11, 18, 29, 47, 76, 123….
Now if we take for starting numbers 1 and 4, we obtain
1, 4, 5, 9, 14, 23, 37, 60, 97, 157, …
37, 60 and 97, which are coloured in red, are the numbers of the columns in Figure 6 discussed in the text.
Notice that in the latter sequence, the first two numbers 1 and 4 add to 5, the number of the sides in a pentagon. Remarkably, the only other two positive integers that add to 5, 2 and 3, will produce the original Fibonacci series! Indeed, 2 + 3 = 5 and hence we obtain
2, 3, 5, 8, 13, 21, ….
A strange interlink between our sequence and that of Fibonacci, I would say.
A general property of all these sequences is that the ratio of the n + 1st to the nth member approaches the Golden Ratio. The original, let us say the ‘natural’ Fibonacci series leads faster to it compared to the other, ‘artificial’, sequences.
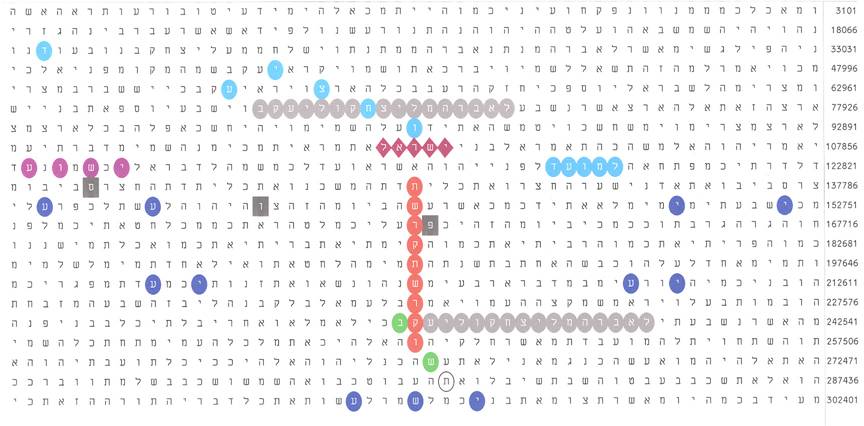
Figure 1.

Figure 2.
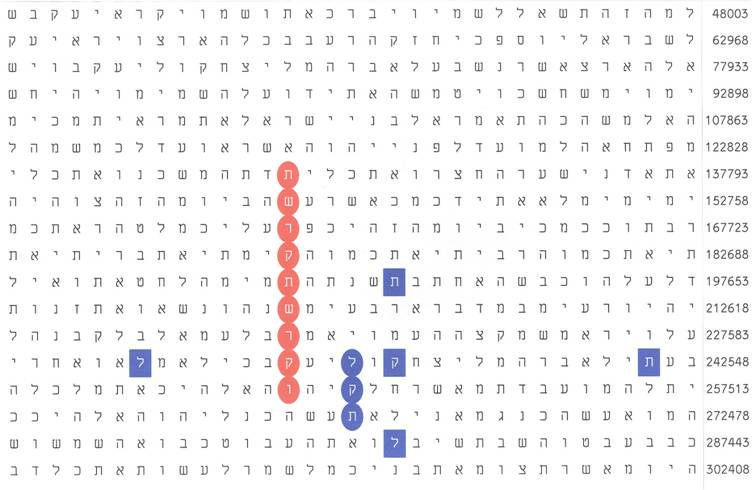
Figure 3.

Figure 4.

Figure 5. Regular Pentagon. Regular polygons are those which vertices are equally distant from a central point and therefore lie on a circle.
The sum of the interior angles of a pentagon is 540°. Each interior angle is 108°. The sum of the interior angles of every polygon in the plain is expressed by the general formula 180(n – 2), where n is the number of sides. For a triangle, n = 3, therefore the sum is 180°. For a tetragon, it is 180?2 = 360°, etc.
This shape was thought to be protective against evil powers by the ancients. Therefore, they constructed their fortresses in the form of pentagons. The most famous contemporary building having this shape is the Pentagon in USA.
The regular pentagon is linked in a strange way with the planet Venus as well. It is an astronomical fact that Venus passes through five fixed points on the celestial sphere every 8 years with a striking accuracy of timing.
The ratio of the length of a diagonal (one of the five diagonals is shown above) to a side in a regular pentagon is exactly the Golden Ratio. These lengths are incommensurate. This means that no unit of length exists, which projects both on the diagonal and the side. The absence of such unit defines irrational numbers.
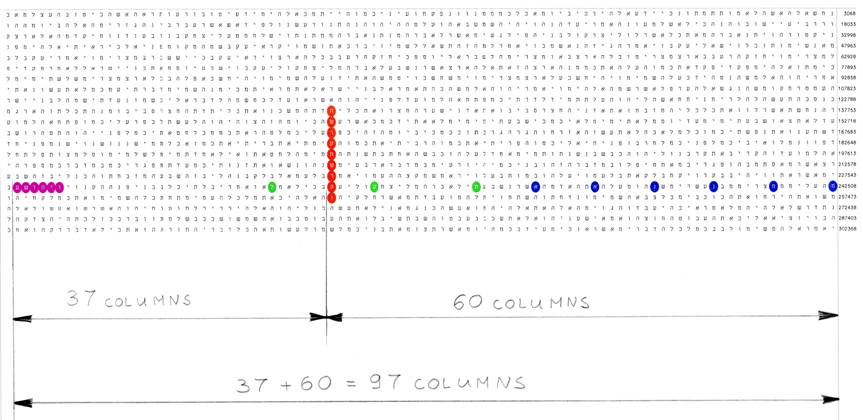
Figure 6.

